Beam Test Results

Two PHOS FEE boards were used for MPC readout. PHOS FEE reshapes analog signal from preamplifiers and digitizes resulting analog amplitude every 10ns 115 times. Digitized samples are used for initial amplitude and time reconstruction.
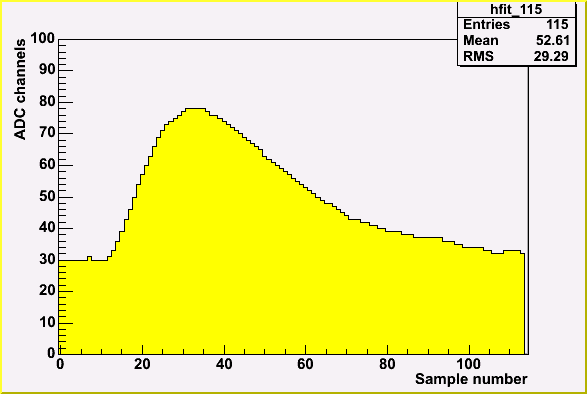
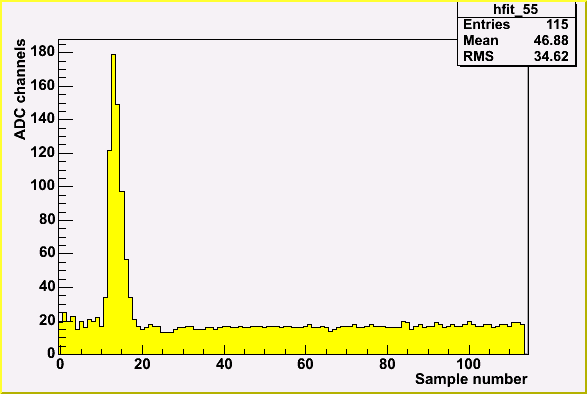
One of boards was modified in order to decrease shaper rise and decay times. Typical samples for modified and original boards are below.

Typical sample in original board	Typical sample in modified board

It was found that test bench picks up noise of high frequency during short periods of time. The source of this noise remains unknown. Probably it is due to poor grounding as the noise of comparable amplitude appears at the same time in all channels except for ones which were not physically connected to preamplifiers.

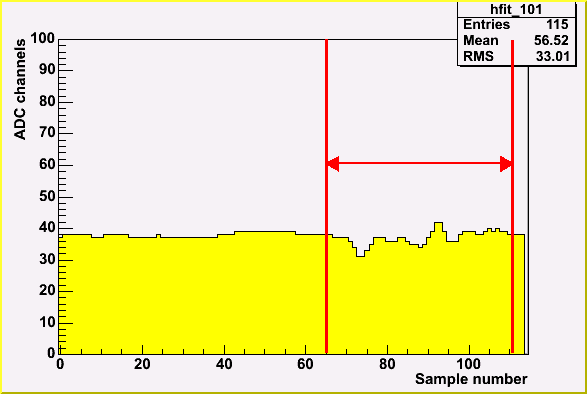
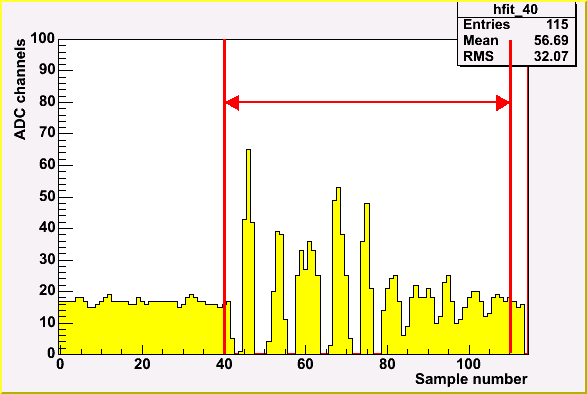
Noise pickup in original board	Noise pickup in modified board

The start point of noise (the first sample in which noise appear) is independent on beam injection time. Threshold on start point cuts off 23% events.

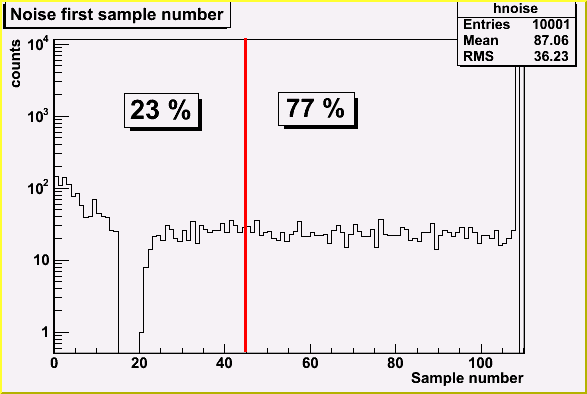Noise start point distribution

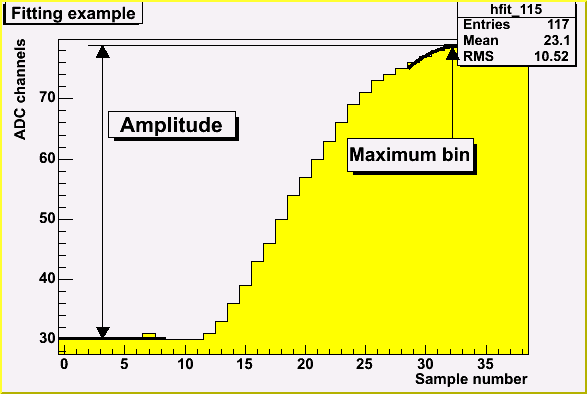
Proposed by PHOS amplitude reconstruction proved to be non-working in our conditions. Therefore amplitude reconstruction was performed by fitting first 7 samples with a constant and +-3 bins around maximum sample with a parabola.

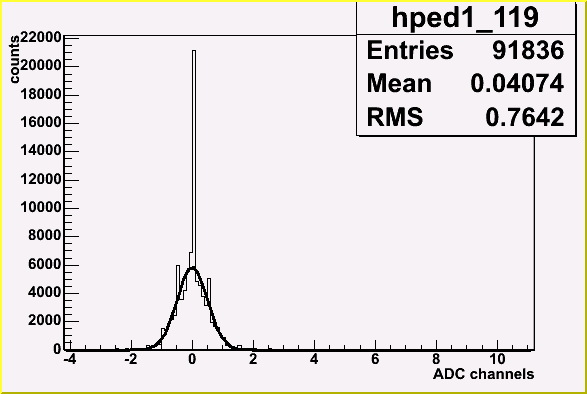
The test beam setup also picks up 50 Hz as it was found at BNL testbench. Therefore pedestal baseline floats more than it can be expected from deviation of samples from average pedestal in one event. Due to this fact pedestals were calculated in each event. Pedestal determination error is 0.29 ADC channels for HG and 0.15 ADC channels for LG.
On the plots below is the following. Plots on the right are distribution of average pedestal value. Plots on the right are distribution of difference of pedestal samples and average pedestal in a event.

Distribution of HG pedestal samples relative to average HG pedestal in one event	Distribution of HG mean pedestal value (typical channel)

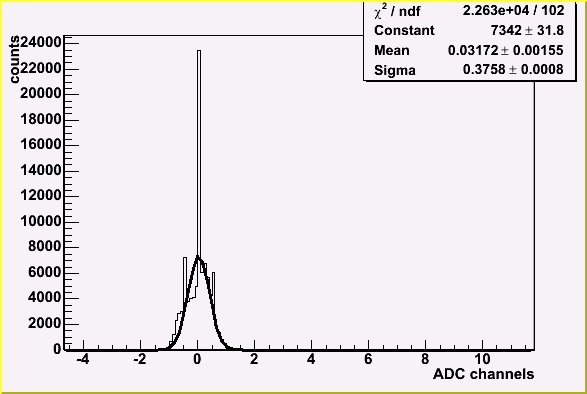
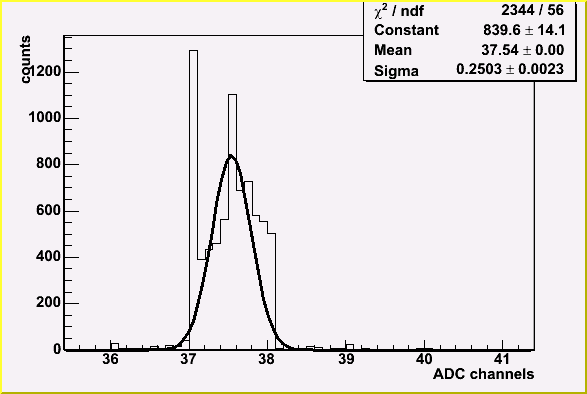
Distribution of LG pedestal samples relative to average HG pedestal in one event	Distribution of LG mean pedestal value (typical channel)

Fitting the maximum of sample with parabola introduces additional error 0.1 ADC channels for LG and HG. After scaling HG to LG final error is 0.3 ADC channels for LG and HG.

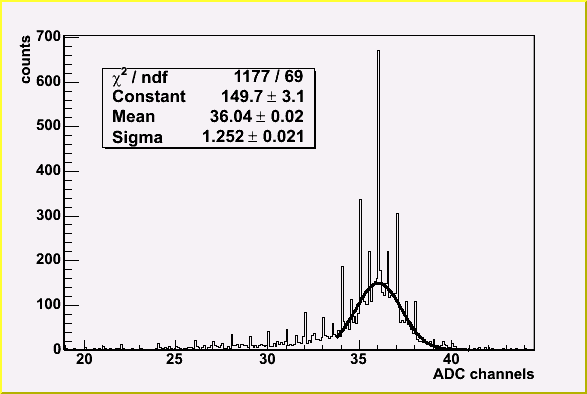
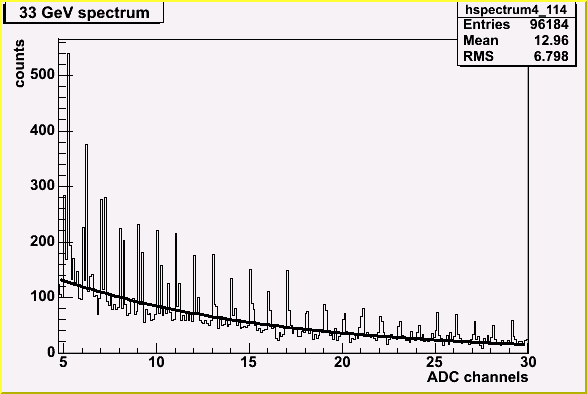Typical reconstructed spectrum

Initially gains were set to be approximately equal using UIUC testbench data. In UIUC tests assembled modules were lit by the same LED and HV was chosen so that all modules give the same amplitude.

Gains were extracted using 2 steps calibration procedure on 16 GeV electrons. Initial gain values were found by the right edge of energy spectrum in each module. The second step was interational adjustment of gains using the position of maximum of 3x3 energy sum around given module.

Final difference of 3x3 energy sum peak position in different modules was less than 1%.

More than 80% of modules are less than 10% off the average value. That means that setting initial gains with LED is a good idea.

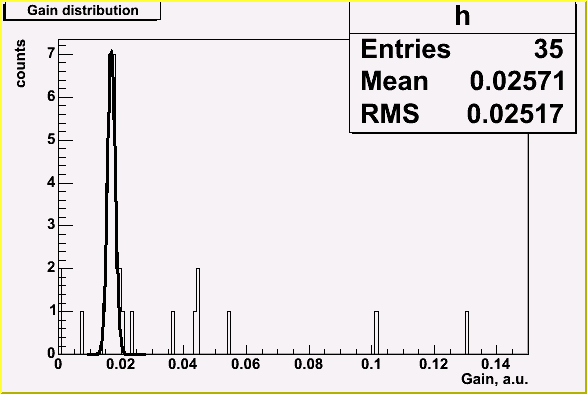Gain distribution

Hi/Lo ratios were extracted from the data on sample by sample basis. The average value of HG_sample/LG_sample(LG_sample) was fitted by a parabola. It is important that fitting by a line gives bad results. HiLo has a significant curvature. It might be effect of non-linearity of HG_digital(HG_analog) at high HG. But it might be more of interest for ALICE guys.
Below is the distribution of linear term of HiLo.

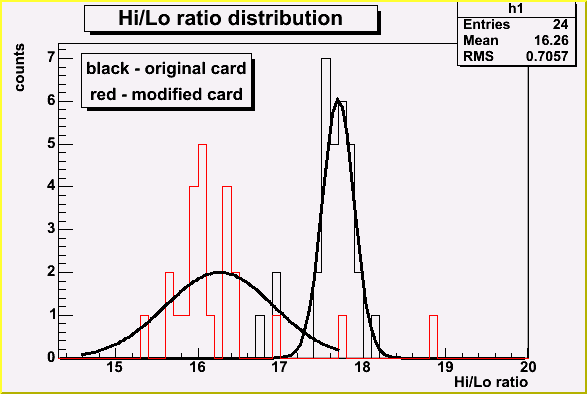HiLo distribution

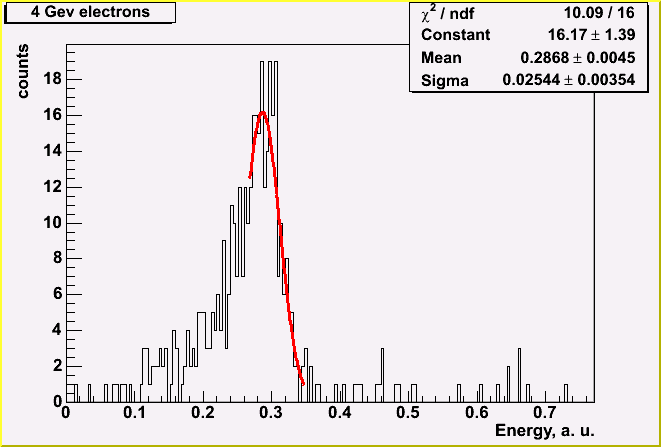
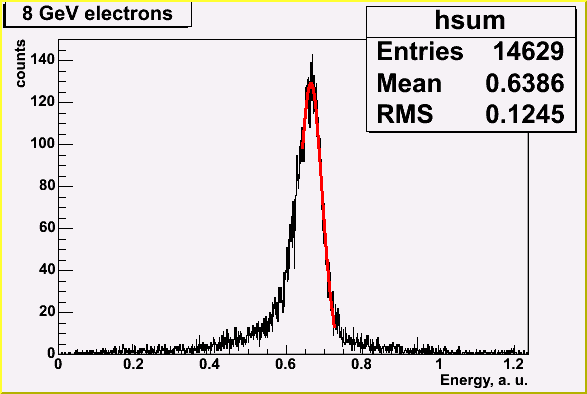
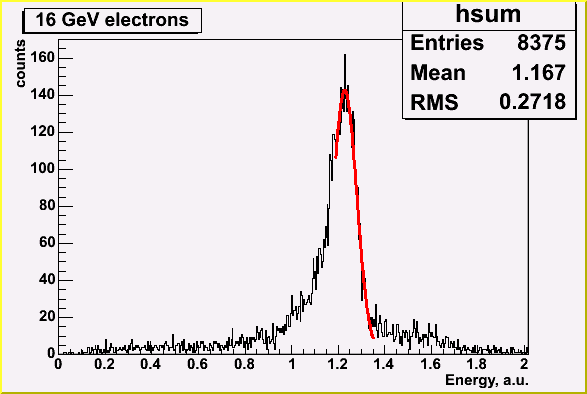
Electrons of 4, 8, 16 and 33 GeV were used for resolution studies. No significant electron peak at 66 GeV and higher were found even after dispersion cut.

4 GeV electrons	8 GeV electrons	16 GeV electrons

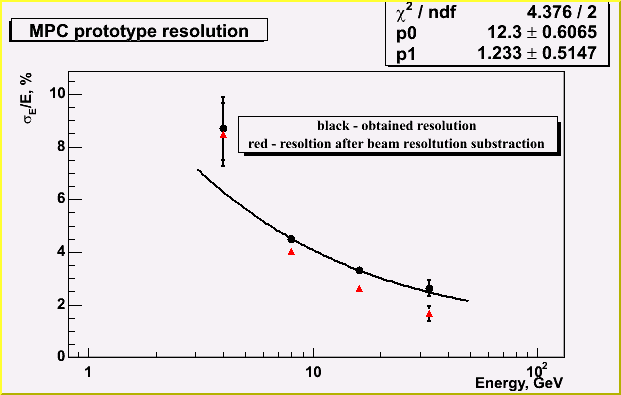
Resolution function was fitted with sigma/E=sqrt((a*a)/E+b*b), where a=12.3 %*sqrt(GeV) and b=1.2%. These values are higher than expected but they include beam resolution and temperature variation - two most significant sources of error in our case.

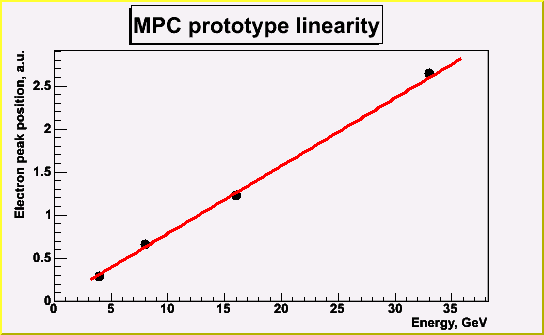
Calculated linearity is quite poor but again assuming beam resolution and temperature variation it might be much better.

Hit point was reconstructed using log weights with w0=4.0. Resulting shower shapes are below.

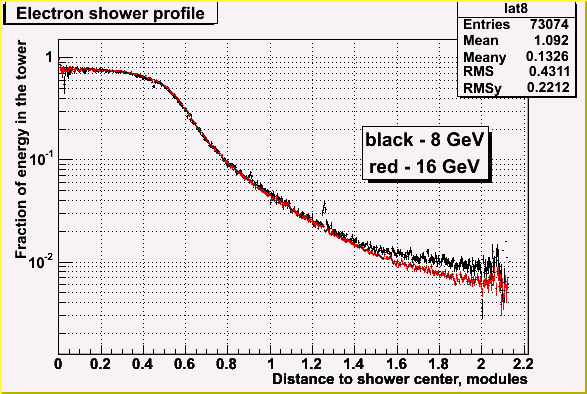
Electron shower shapes at 8 and 16 GeV start to differ from distance from center of the shower of approximately 1.4 which corresponds to approximately 1% of shower energy. It can be explained by the relative noise level which is two times higher for 8 GeV as compared to 16 GeV.

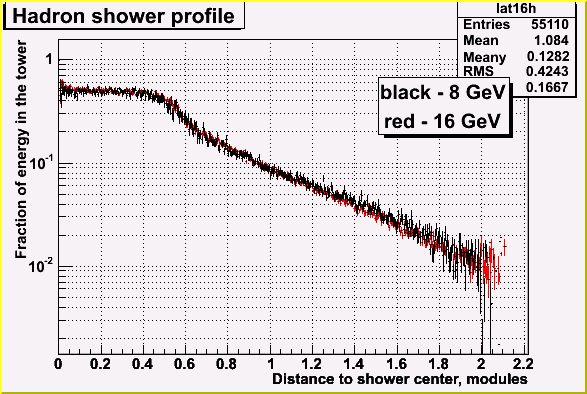
In fact it not a shape of pure hadron sample. It contains significant ammount of misidentified electrons which contribute to the "bump" below 0.5 modules.

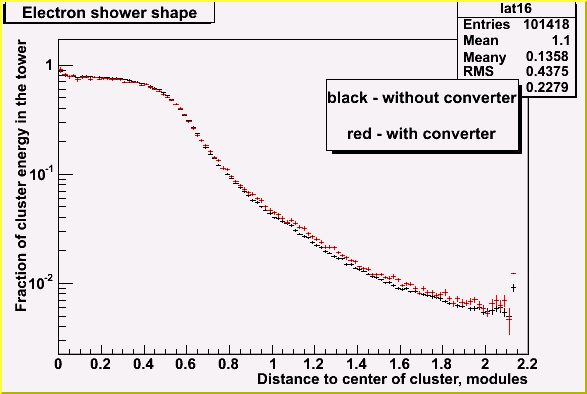
Aluminum converter installed in front of MPC prototype for studies of BBC influence on MPC gave not a significant increase of shower width. Average dispersion width increased by less than 1%.

Modified card is more sensitive to high frequency noise. As it appears it has a strong influence on dispersion resolution.

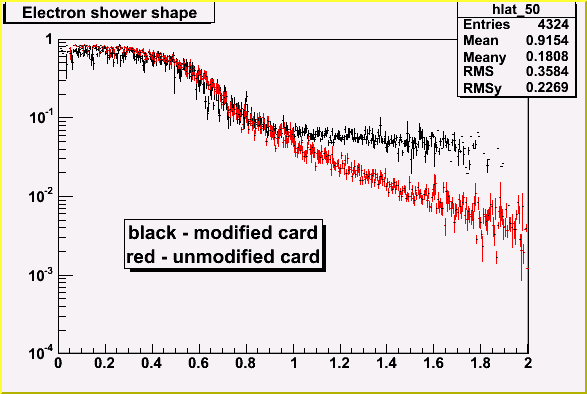
In modified card noise becomes larger than energy deposit starting from distance of 0.8 modules from the center of the shower. It means that only 3 tower energies can be used for hit point and dispersion reconstruction.

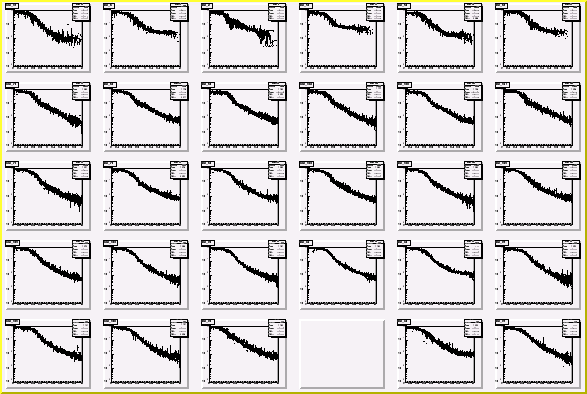Shower shapes module-by-module in the central part of MPC prototype

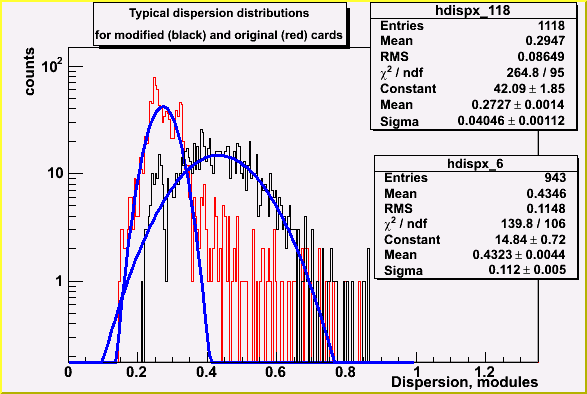
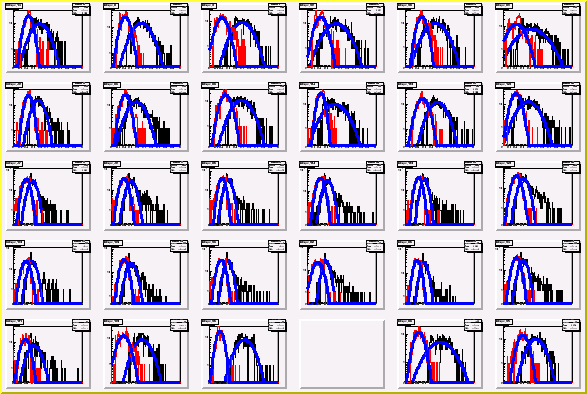Dispersion along pricipal axes distribution in central modules of MPC prototype.
Black - maximum dispersion distribution
Red - miminum dispersion distribution